2025年成考高起点每日一练《数学(理)》5月5日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、（）。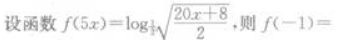

• A：
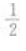
• B：
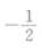
• C：2
• D：－2

答 案：B

解 析：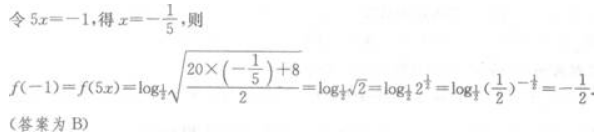

2、教室里有50人在开会，其中学生35人，家长12人，老师3人，若校长站在门外听到有人发言，那么发言人是老师或学生的概率为（）。

• A：
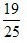
• B：
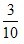
• C：
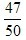
• D：

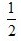
答 案：A

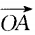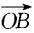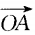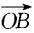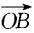3、已知=（3，2），=（-4，y），并其人⊥，则的长度为（）。

• A：
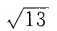
• B：
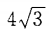
• C：
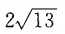
• D：

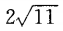
答 案：C

解 析：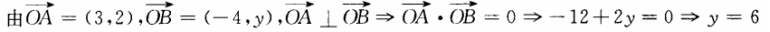

4、一个袋子中装有标号分别为1，2，3，4的四个球，采用有放回的方式从袋中摸球两次，每次摸出一个球，则恰有一次摸出2号球的概率为（）。

• A：
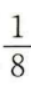
• B：
• C：
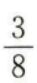
• D：

答 案：C

解 析：本题主要考查的知识点为独立重复试验的概率。 所求概率为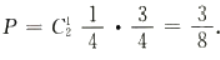

主观题

1、计算。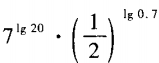  

答 案：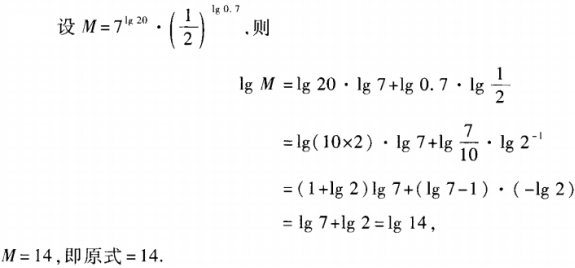

2、空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?  

答 案：根据公理，在所给定的四点中任取三点，可确定一个平面，由组合公式所以共可确定四个平面。

解 析：空间有n个点，如果其中任何三点不在同一直线上，可以确定个平面。  

3、已知函数f(x)=(x-4)(x²-a) （I）求f"(x)； (Ⅱ)若f"(-1)=8，求f(x)在区间[0，4]的最大值与最小值

答 案：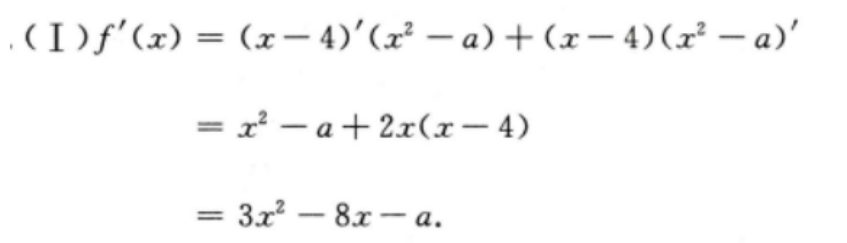

4、（1）已知tanα=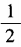，求cot2α的值； （2）已知tan2α=1，求tanα的值。

答 案：（1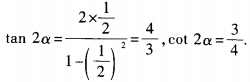）（2）由已知，得 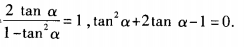解关于tanα的一元二次方程，得tanα=  

填空题

1、lgsinθ=a,lgcosθ=b，则sin2θ=______。  

答 案：2×10^a+b

解 析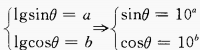： sin2θ=2sinθcosθ=2×10^a×10^b=2×10^a+b  

2、曲线y=在点(1，1)处的切线方程是______。

答 案：2x+y-3=0

解 析：本题主要考查的知识点为切线方程 由题意，该切线斜率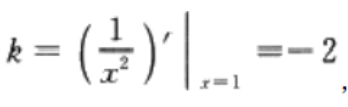， 又过点(1，1)，所以切线方程为y-1=-2(x-1)