2025年成考专升本每日一练《高等数学一》5月3日专为备考2025年高等数学一考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、若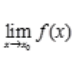 存在,
存在,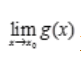 不存在,则()。
不存在,则()。
- A:
 与
与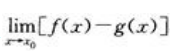 都不存在
都不存在 - B:
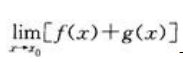 与
与 都存在
都存在 - C:
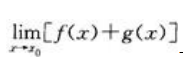 与
与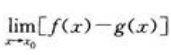 之中的一个存在
之中的一个存在 - D:
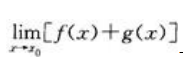 存在与否与f(x),g(x)的具体形式有关
存在与否与f(x),g(x)的具体形式有关
答 案:A
解 析:根据极限的四则运算法则可知: ,
,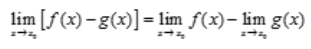 ,所以当
,所以当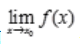 存在,
存在,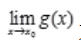 不存在时,
不存在时,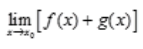 ,
,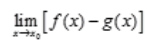 均不存在。
均不存在。
2、微分方程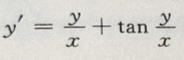 的通解为()
的通解为()
- A:
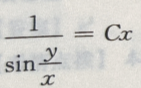
- B:
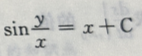
- C:
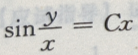
- D:
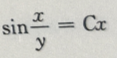
答 案:C
解 析:设 代入有
代入有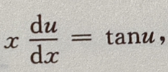 所以
所以
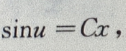 原方程的通解为
原方程的通解为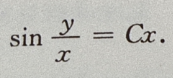
3、设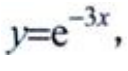 则dy=()。
则dy=()。
- A:
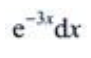
- B:
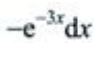
- C:
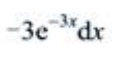
- D:
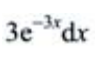
答 案:C
解 析: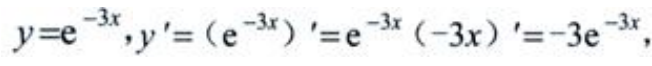 故
故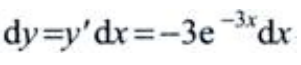 .
.
主观题
1、若 ,求a与b的值。
,求a与b的值。
答 案:解: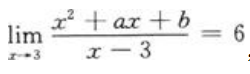 ,又x
,又x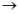 3,分母x-3
3,分母x-3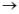 0;所以
0;所以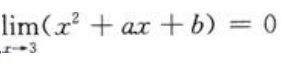 ,得9+3a+b=0,b=-9-3a,则
,得9+3a+b=0,b=-9-3a,则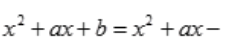 (9+3a)=(x-3)[x+(3+a)],故
(9+3a)=(x-3)[x+(3+a)],故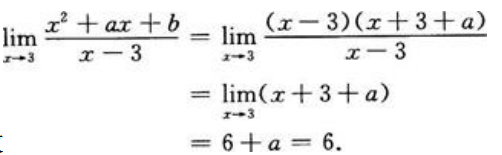 a=0,b=-9。
a=0,b=-9。
2、设z=xy2+eycosx,求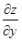 .
.
答 案:解:z=xy2+eycosx,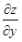 =2xy+eycosx。
=2xy+eycosx。
3、已知f(π)=1,且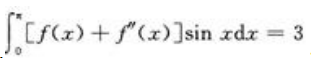 ,求f(0)。
,求f(0)。
答 案:解:
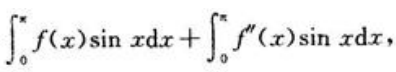 对
对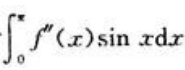 采用凑微分和分部积分后与
采用凑微分和分部积分后与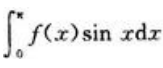 相加,代入条件即可求出f(0)。因为
相加,代入条件即可求出f(0)。因为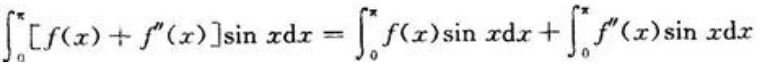
而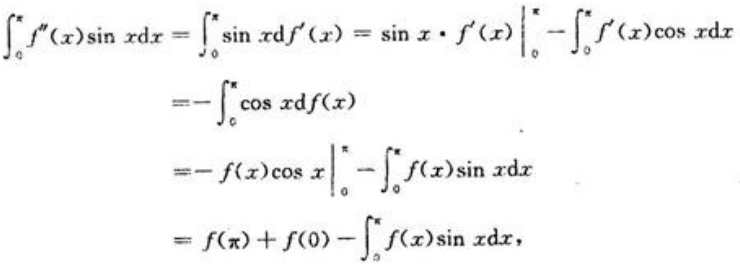
所以
又f(π)=1,所以f(0)=2。
填空题
1、反常积分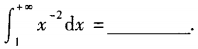
答 案:1
解 析:本题考查的知识点为反常积分,应依反常积分定义求解。 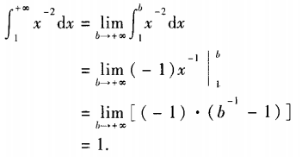
2、设y=sin(2+x),则dy=()。
答 案:cos(2+x)dx。
解 析:这类问题通常有两种解法: 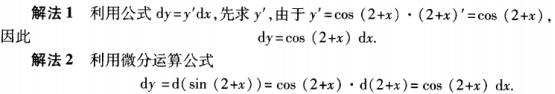
3、曲线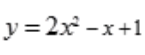 在点(1,2)处的切线方程为()。
在点(1,2)处的切线方程为()。
答 案:y-2=3(x-1)
解 析:y=2x2-x+1点(1,2)在曲线上,且 ,因此曲线过点(1,2)的切线方程为y-2=3(x-1),或写为y=3x-1。
,因此曲线过点(1,2)的切线方程为y-2=3(x-1),或写为y=3x-1。
简答题
1、计算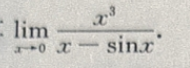
答 案: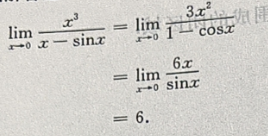
精彩评论