2025年高职单招每日一练《数学(中职)》4月30日专为备考2025年数学(中职)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、“x为有理数”是“x²为有理数”的（）  

• A：充分不必要条件
• B：必要不充分条件
• C：充要条件
• D：既不充分也不必要条件

答 案：A

解 析：x为有理数，则x²一定为有理数，但x²为有理数，x不一定为有理数，比如3为有理数，但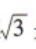 是无理数，所以“x为有理数”是“x²为有理数”的充分不必要条件.

2、若f(x)=2x²+ax+1是R上的偶函数，则f(x)在区间[-3,2]上的最小值为()

• A：0
• B：1
• C：9
• D：19

答 案：B

解 析：因为f(x)=2x²+ax+1是R上的偶函数，所以f(-x)=f(x),即2(-x)²-ax+1=2x²+ax+1,解得a=0,所以f(x)=2x²+1.因为函数f(x)=2x²+1的图象开口向上，且对称轴为y轴，所以f(x)在[-3,0]上单调递减，在[0,2]上单调递增，函数f(x)的最小值为f(0)=1.

3、已知A(5,-4),B(3,-6),则线段AB的中点坐标为()  

• A：(4,-5)
• B：(4,5)
• C：(-4,-5)
• D：(-5,4)

答 案：A

解 析：设线段AB的中点坐标为(x,y).因为A(5,-4)，B(3,-6)，所以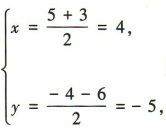所以线段AB的中点坐标为(4,-5).

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、已知扇形的面积为4,圆心角为2rad,则该扇形的周长为（）  

答 案：8

解 析：扇形的半径为r.由扇形的面积为4,圆心角α=2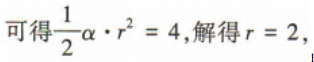 所以扇形的弧长l=α·r=4,所以扇形的周长为l+2r=8.

2、tan(-390°)=（）  

答 案：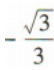

解 析：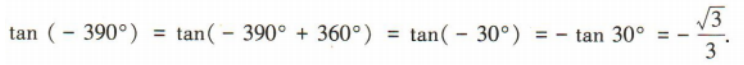

3、在等比数列{an}中，a₁=1,a₂=3,则a₅=（）

答 案：81

解 析：

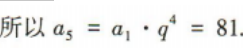
简答题

1、求函数f(x)=x3-3x2-9x+5的单调区间，极值.  

答 案：解:f’(x)=3x²-6x-9=3(x+1)(x-3) 令f’(x）＞0，x＞3或x<-1 令f’(x)＜0，-1＜x＜3 ∴f(x)单调增区间为(-∞，-1]，[3,+∞) 单调减区间为[-1，3] f(x)极大值为f(-1)=10 f(x)极小值为f(3)=-22