2025年成考高起点每日一练《数学(理)》4月29日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、一个袋子中装有标号分别为1,2,3,4的四个球,采用有放回的方式从袋中摸球两次,每次摸出一个球,则恰有一次摸出2号球的概率为()。
- A:
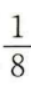
- B:

- C:
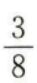
- D:

答 案:C
解 析:本题主要考查的知识点为独立重复试验的概率。 所求概率为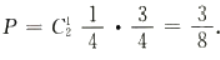
2、设log57=m,log25=n,则log27=()。
- A:
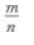
- B:
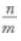
- C:m+n
- D:m·n
答 案:D
解 析: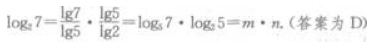
3、若tan(π-α)>0,且cosα>0,则α的终边在()。
- A:第一象限
- B:第二象限
- C:第三象限
- D:第四象限
答 案:D
解 析:∵tan(π-α)>0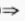 -tanα>0
-tanα>0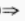 tanα<0,且cosα>0∴α在第四象限。
tanα<0,且cosα>0∴α在第四象限。
4、函数F(x)=f(x)·sinx是奇函数,则f(x)()。
- A:是偶函数
- B:是奇函数
- C:既是偶函数又是奇函数
- D:既不是偶函数又不是奇函数
答 案:A
解 析:因为函数F(x)=f(x)·sinx是奇函数,sinx是奇函数, 故 F(-x)=-F(x),sin(-xx)=-sinx. 即f(x)sin(-x)=-f(x)sinx,得f(x)=f(-x),则f(x)是偶函数(答案为 A)
主观题
1、设a为实数,且tanα和tanβ是方程ax2+(2a-3)x+(a-2)=0的两个实根,求tan(α+β)的最小值。
答 案:由已知得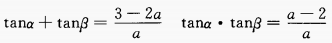

2、求(1+tan10°)(1+tan35°)的值。
答 案:原式=1+tan10°+tan35°+tan10°·tan35°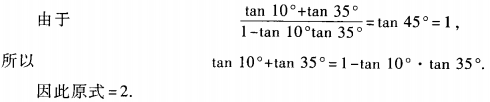
3、在△ABC中如果sinA=2sinBcosC,求证:△ABC是等腰三角形。
答 案: ∴△ABC为等腰三角形。
∴△ABC为等腰三角形。
4、cos20°cos40°cos80°的值。
答 案:
填空题
1、已知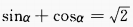 ,则
,则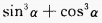 =______。
=______。
答 案:
解 析:

2、若平面向量a=(x,1),b=(1,-2),且a//b,则x=()
答 案: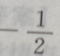
解 析:由于a//b,故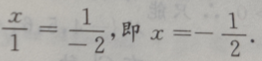
精彩评论