2025年成考专升本每日一练《高等数学二》4月28日专为备考2025年高等数学二考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、若，则。（）  

答 案：错

解 析：

单选题

1、过曲线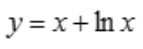上点M₀的切线平行于直线y＝2x＋3，则切点M₀的坐标是（）.

• A：（1，1）
• B：（e，e）
• C：（1，e＋1）
• D：（e，e＋2）

答 案：A

解 析：因为M₀的切线平行于直线y＝2x＋3,故函数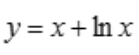在点M₀处的导数应该为2，又因为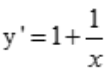，所以得到x的值为1，代入原式可求得y的值为1.

2、设函数f（x）=arctanx，则（）

• A：arctanx+C
• B： -arctanx +C
• C：
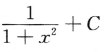
• D：

答 案：A

解 析：

主观题

1、某射手击中10环的概率为0.26，击中9环的概率为0.32，击中8环的概率为0.36，求在一次射击中不低于8环的概率．

答 案：解：设A＝{击中10环），B＝{击中9环），C＝{击中8环），D＝{击中不低于8环），则D＝A＋B＋C，由于A，B，C相互独立，所以P（D）＝P（A＋B＋C）＝P（A）＋P（B）＋P（C）＝0.26＋0.32＋0.36＝0.94

2、（1）求在区间[0，π]上的曲线y＝sinx与x轴所围成图形的面积A；（2）求（1）中的平面图形绕x轴旋转一周所得旋转体的体积V_x．

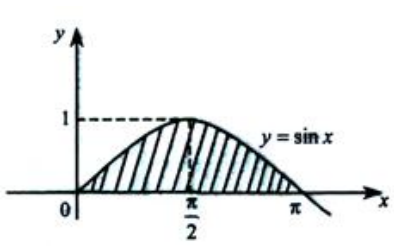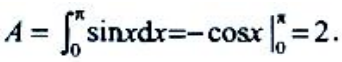答 案：解：平面图形如下图阴影部分．（1）（2）

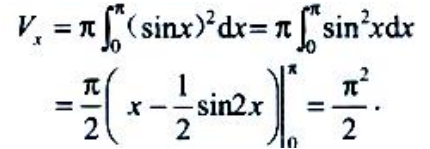
填空题

1、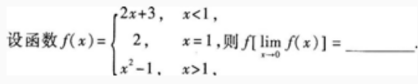  

答 案：8

解 析：因为则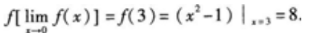

2、设事件A与B相互独立，且P(A)＝0.4，P(A＋B)＝0.7，则P(B)＝（）．

答 案：0.5

解 析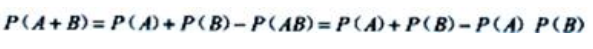：．即0.7＝0.4＋P(B)－0.4P(B)．得P(B)＝0.5．

简答题

1、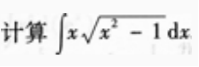  

答 案：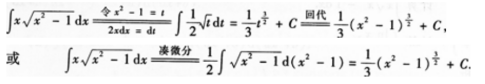

2、  

答 案：。