2025年高职单招每日一练《数学》4月27日专为备考2025年数学考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、已知等差数列的前四项依次为10,7,4,1,则该数列的第10项是-14.()  

答 案：错

解 析：由题意可知d=-3，a1=10，所以a10=a1+9d=10-27=-17

2、零和负数没有对数。（）  

答 案：对

解 析：零没有对数。在实数范围内,负数无对数。

单选题

1、函数f(x)=2x是()  

• A：奇函数
• B：偶函数
• C：非奇非偶函数
• D：既是奇函数又是偶函数

答 案：A

解 析：∵f(x)=2x，f(-x)=2（-x）=-2x，∴f(-x)=-f(x)，则函数为奇函数

2、已知点A(2,1),F是抛物线y²=4x的焦点，P为抛物线上的一点，则|PA|+|PF|的最小值是().

• A：2
• B：3
• C：4
• D：5

答 案：B

解 析：设点P在准线上的射影为D,则根据抛物线的定义可知|PF|=|PD|,要求|PA|+|PF|取得最小值，即求|PA|+|PD|取得最小值.当D,P,A三点共线时，|PA|+|PD|最小.由点A坐标为(2,1),抛物线y²=4x的准线方程为x=-1,故此时|PA|+|PD|=|AD|=2-(-1)=3.故选B

多选题

1、下列命题中，不正确的是（）  

• A：三点可确定一个圆
• B：三角形的外心是三角形三边中线的交点
• C：一个三角形有且只有一个外接圆
• D：三角形的外心必在三角形的内部或外部

答 案：ABD

解 析：A、不在同一条直线上的三点确定一个圆，故本选项错误；B.、三角形的外心是三角形三边垂直平分线的交点，所以本选项是错误；C、三角形的外接圆是三条垂直平分线的交点，有且只有一个交点，所以任意三角形一定有一个外接圆，并且只有一个外接圆，所以本选项是正确的；D、直角三角形的外心在斜边中点处，故本选项错误。故选：ABD

2、已知函数y=1/2sin2x则（）  

• A：函数最大值为2
• B：函数最大值为1/2
• C：周期
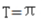
• D：周期

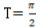
答 案：BC

解 析：A：sin2x最大值为1，则y=1/2sin2x的最大值为1/2，故A错B对。C：T=2π/W=2π/2=π，故C对D错

主观题

1、已知等差数列{an}的前n项和S_n且S₅=35,S₈=104.
(1)求数列{an}的通项公式；
(2)若{b_n}为等比数列，b₁=a₂,b₂=a₃+2,求数列{b,}的公比q及前n项和T_n.

答 案：(1)所以a₆=19.则数列{an}的公差，通项公式为an=a₆+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以则

2、已知函数f(x)=log₃(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.

答 案：(1)根据题意可得，3x-1>0,解得所以函数f(x)的定义域是(2)因为f(x)=log₃(3x-1)<1=log₃3,f(x)为定义域上的增函数，所以O<3x-1<3,解得所以x的取值范围是

填空题

1、在数列{a_n}中， a₂=2,a₁₇=66,通项公式是项数n的一次式，则 a_n=______ .

答 案：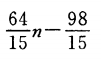

2、如果函数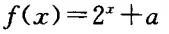的图像经过点（2,7），则f(3)=______。  

答 案：11