2025年成考高起点每日一练《数学(理)》4月12日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、设f(x)是以7为周期的偶函数，且f(-2)＝5，则f(9)＝（）。

• A：-5
• B：5
• C：-10
• D：10

答 案：B

解 析：因为f(x)是偶函数，所以f(2)＝f(-2)＝5，又因为f(x)是以7为周期的函数，则f(9)＝f(7＋2)＝f(2)＝5。答案为B。

2、下列各式中，不成立的是（）。

• A：
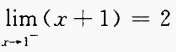
• B：
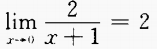
• C：
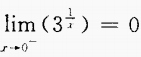
• D：

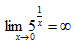
答 案：D

解 析：可用排除法，A、B、C均成立。

3、（）。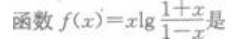  

• A：奇函数
• B：偶函数
• C：非奇非偶函数
• D：无法判断

答 案：B

解 析：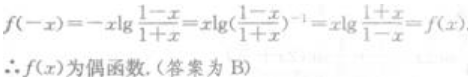

4、已知3sin²α+8sinα-3=0，则cos2α=（）。

• A：
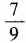
• B：
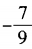
• C：
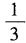
• D：

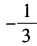
答 案：A

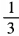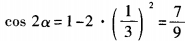解 析：由已知得（3sinα-1）（sinα+3）=0。 由于|sinα|≤1，所以sinα=。因此。故选A。

主观题

1、已知a,b,c成等差数列，a,b,c+1成等比数列．若b=6，求a和c．

答 案：由已知得解得

2、已知x+x^-1=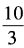，求x²+x-2的值。

答 案：由已知，得

3、设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
(II）求f（x）的极值．

答 案：(I）f(1)=1,f'(x)=2+lnx，故f'(1)=2.所以曲线y=f(x）在点（1,f(1))处的切线方程为y=2x-1.(II）令f'(x)=0，解得当时，f'(x)时，f'(x)＞O.故f(x）在区间单调递减，在区间单调递增．因此f(x）在时取得极小值

4、已知空间四边形OABC，OB=OC且∠AOB=∠AOC=θ（如图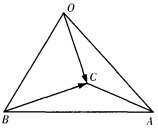）。求证：OA⊥BC。

答 案：

填空题

1、函数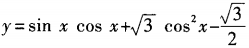（x∈R）的最小值为______。

答 案：-1

解 析：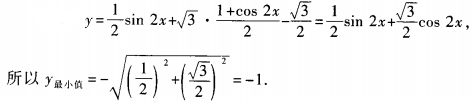

2、函数y=x⁴-2x²+5,x∈[-2,2]上的最小值______，最大值______。

答 案：4；13

解 析：y=x⁴-2x²+5,y'=4x³-4x