2025年成考高起点每日一练《数学(文史)》4月7日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、下列函数中,为奇函数的是()。
- A:y=log3x
- B:y=3x
- C:y=3x2
- D:y=3sinx
答 案:D
2、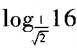 =()。
=()。
- A:8
- B:-8
- C:2
- D:-2
答 案:B
解 析:由于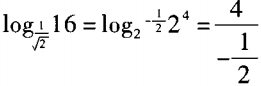 。log22=-8。故选B。
。log22=-8。故选B。
3、△ABC中,已知AC=12,∠A=30°,∠B=120°,则BC=()
- A:
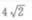
- B:
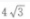
- C:
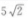
- D:
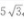
答 案:B
4、某单位有4名男同志和3名女同志,现要组成一个有男有女的小组,规定小组中男同志的数目为偶数,女同志的数目为奇数,则共有组织方法种数是( )
- A:18种
- B:28种
- C:36种
- D:324种
答 案:B
解 析:首先确定这是一个组合问题,因为组成小组的人员与排列顺序无关.其次按照题意可知:虽然组成小组的人数可以不限,但必须同时有男同志和女同志,而且男同志人数必须为偶数,女同志人数必须为奇数.由此可知:当男同志为2人时,女同志可为1人或3人,当男同志为4人 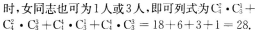 【考点指要】本题考点在于会正确判断给定问题是排列问题还是组合问题,并且会解排列、组合的简单应用题.排列、组合的简单应用题是近几年成人高考的必考内容.
【考点指要】本题考点在于会正确判断给定问题是排列问题还是组合问题,并且会解排列、组合的简单应用题.排列、组合的简单应用题是近几年成人高考的必考内容.
主观题
1、求下列函数的最大值、最小值和最小正周期: (1)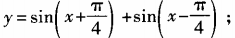 2)y=6cosx+8sinx
2)y=6cosx+8sinx
答 案: 所以函数的最大值是
所以函数的最大值是 最小值是
最小值是 最小正周期为2π,
(2)要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式,需使cosx与sinx的系数平方和为1,为此,将已知函数化为
最小正周期为2π,
(2)要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式,需使cosx与sinx的系数平方和为1,为此,将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π
因此,函数的最大值是10,最小值是-10,最小正周期为2π
2、已知函数f(x)=(x-4)(x2-a)。(I)求f’(x);
(Ⅱ)若f’(-1)=8,求f(x)在区间[0,4]的最大值与最小值。
答 案:(I)f'(x) =(x-4)'(x2-a)+(x-4)(x2-a)’
=x2-a+2x(x-4)
=3x2-8x-a.
(Ⅱ)由于f’(-1)=3+8-a=8,得a=3.
令f'(x)=3x2-8x-3=0,解得x1=3, (舍去)又f(0)=12,f(3)=-6,f(4)=0所以在区间[0,4]上函数最大值为12,最小值为-6
(舍去)又f(0)=12,f(3)=-6,f(4)=0所以在区间[0,4]上函数最大值为12,最小值为-6
3、求证:双曲线的一个焦点到一条渐近线的距离等于虚半轴的长.
答 案:设双曲线的方程为 则它的焦点坐标为F1(-c,0),F2(c,0),其中c2=a2+b2,渐近线方程为
则它的焦点坐标为F1(-c,0),F2(c,0),其中c2=a2+b2,渐近线方程为 令设焦点F2(c,0)到渐近线
令设焦点F2(c,0)到渐近线 的距离为d,则
的距离为d,则 即从双曲线
即从双曲线 的一个焦点F2(c,0)到一条渐近线
的一个焦点F2(c,0)到一条渐近线 的距离等于虚半
轴的长b,由上述推导过程可知,点F2到渐近线
的距离等于虚半
轴的长b,由上述推导过程可知,点F2到渐近线 以及点F1(-c,0)到渐近线
以及点F1(-c,0)到渐近线 的距离都等。
由于证明中只涉及a,b,c,而与双曲线的位置无关,所以这个结论对于任意双曲线都成立.
的距离都等。
由于证明中只涉及a,b,c,而与双曲线的位置无关,所以这个结论对于任意双曲线都成立.
解 析:本题考查的是圆锥曲线与直线位置关系的推理能力,主要是用代数的方法表示几何中的问题.考生必须对曲线方程、几何性质及元素之间的关系有深刻的理解,方可解决此类综合题.这种综合性的圆锥曲线试题出现的概率比较高,要引起重视.
4、已知tan2θ=2tan2ψ+1,求cos2θ+sin2ψ的值。
答 案:由已知,得 
填空题
1、已知向量a=(3,2),b=(-4,x),且a⊥b,则x=()
答 案:6
解 析:∵a⊥b, ∴3×(-4)+2x=0 ∴x=6.
2、已知10x=3,10y=4,则103(x-y)的值等于______。
答 案: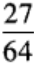
解 析:由已知,103x=27,103y=64,原式=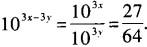
精彩评论