2025年成考高起点每日一练《数学(文史)》4月6日专为备考2025年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、若向量a=(1,-1),b=(1,x),且|a+b|=2,则x=()。
- A:-4
- B:-1
- C:1
- D:4
答 案:C
解 析: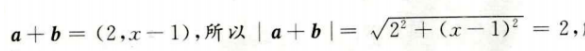 解得x=1 本题主要考查的知识点为向量的加法和模。
解得x=1 本题主要考查的知识点为向量的加法和模。
2、函数y=x2+1(x>0)的图像在()
- A:第一象限
- B:第二象限
- C:第三象限
- D:第四象限
答 案:A
解 析:当x>0时,函数y=x2+1>0,因此函数的图像在第一象限.
3、设集合M={1,2,3,4,5},N={2,4,6},T={4,5,6}则(M∩T)∪N是()。
- A:{2,4,5,6}
- B:{4,5,6}
- C:{1,2,3,4,5,6}
- D:{2,4,6}
答 案:A
4、用0,1,2,3这四个数,组成的没有重复数字的四位数的共有()。
- A:24个
- B:18个
- C:12个
- D:10个
答 案:B
主观题
1、已知a-a-1=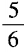 ,求a3-a-3的值。
,求a3-a-3的值。
答 案:
2、若tanα、tanβ是关于x的方程mx2-(2m-3)x+m-2=0的两个实根,求tan(α+β)的取值范围
答 案: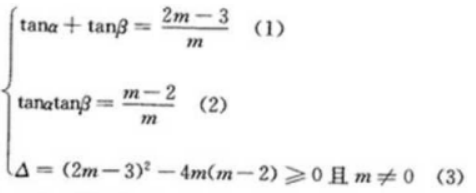 由(1)(2)得,tan(a+β)=m-3/2;由(3)得m≤9/4且m≠0所以tan(a+β)的取值范围是(-∞,-3/2)U(-3/2,3/4)
由(1)(2)得,tan(a+β)=m-3/2;由(3)得m≤9/4且m≠0所以tan(a+β)的取值范围是(-∞,-3/2)U(-3/2,3/4)
3、求(1+tan10°)(1+tan35°)的值。
答 案:原式=1+tan10°+tan35°+tan10°·tan35° 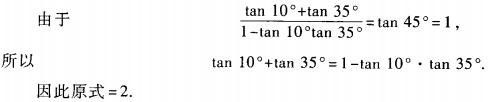
4、已知lg2=a,lg3=b,求lg0.15关于a,b的表达式。
答 案: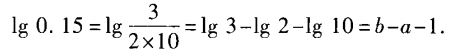
填空题
1、log2[log2(log381)]=______。
答 案:1
解 析:由于log381=log334=4,于是 原式=log2(log24)=log22=1。
2、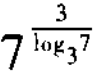 =______。
=______。
答 案:27
解 析: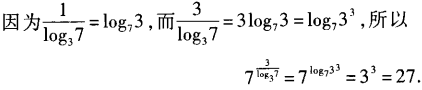
精彩评论