2025年成考专升本每日一练《高等数学一》4月6日专为备考2025年高等数学一考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、设函数f(x)在（0，1）上可导且在[0，1]上连续，且f'(x)＞0，f(0)＜0，f(1)＞0，则f(x)在（0，1）内（）。

• A：至少有一个零点
• B：有且仅有一个零点
• C：没有零点
• D：零点的个数不能确定

答 案：B

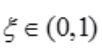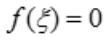解 析：因为函数f(x)在[0，1]上连续，f(0)＜0，f(1)＞0，故存在，使得，又f'(x)＞0，函数在（0，1）上单调增加，故f(x)在（0，1）内有且仅有一个零点。

2、下列函数在指定区间上满足罗尔中值定理条件的是（）。

• A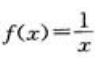：，x∈[2，0]
• B：f(x)＝（x－4）²，x∈[-2，4]
• C：f(x)＝sinx，
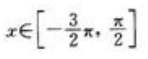
• D：f(x)＝|x|，x∈[-1，1]

答 案：C

解 析：罗尔中值定理条件包括：①在闭区间[a，b]上连续；②在开区间（a，b）内可导；③f（a）＝f（b）.AB两项，条件③均不满足；C项，三个条件均满足；D项，不满足条件②。

3、用待定系数法求方程y''－y＝xe^x的特解时，特解应设为（）。

• A：y＝Ae^-x＋Be^x
• B：y＝（Ax＋B）xe^x
• C：y＝（Ax＋B）e^x
• D：y＝（A＋B）xe^x

答 案：B

解 析：因为该微分方程的特征方程为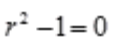，显然该特征方程的根为，故特解应设为。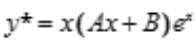

主观题

1、计算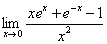

答 案：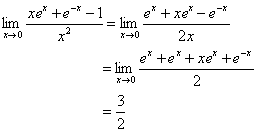

2、求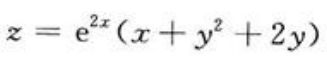的极值．

答 案：解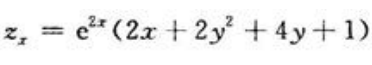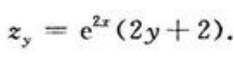：，故由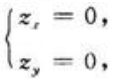得驻点（1/2，－1），于是，且。故（1/2，－1）为极小值点，且极小值为

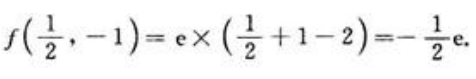
3、曲线y²＋2xy＋3＝0上哪点的切线与x轴正向所夹的角为？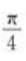

答 案：解：将y²＋2xy＋3＝0对x求导，得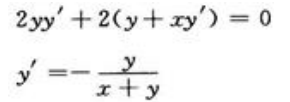欲使切线与x轴正向所夹的角为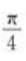，只要切线的斜率为1，即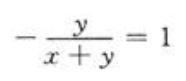亦即x＋2y＝0，设切点为（x₀，y₀），则x₀＋2y₀＝0①
又切点在曲线上，即y₀²＋2x₀y₀＋3＝0②
由①，②得y₀＝±1，x₀＝±2
即曲线上点（－2，1），（2，－1）的切线与x轴正向所夹的角为。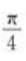

填空题

1、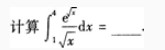  

答 案：2（e²-e）

解 析：

2、＝（）。

答 案：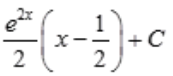

解 析：

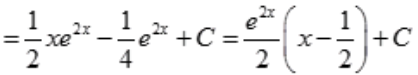
3、  

答 案：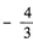

解 析：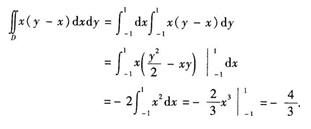

简答题

1、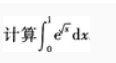  

答 案：