2025年成考专升本每日一练《高等数学二》3月27日专为备考2025年高等数学二考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析:
单选题
1、过曲线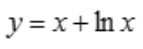 上点M0的切线平行于直线y=2x+3,则切点M0的坐标是().
上点M0的切线平行于直线y=2x+3,则切点M0的坐标是().
- A:(1,1)
- B:(e,e)
- C:(1,e+1)
- D:(e,e+2)
答 案:A
解 析:因为M0的切线平行于直线y=2x+3,故函数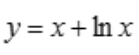 在点M0处的导数应该为2,又因为
在点M0处的导数应该为2,又因为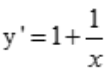 ,所以得到x的值为1,代入原式可求得y的值为1.
,所以得到x的值为1,代入原式可求得y的值为1.
2、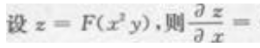 ()。
()。
- A:
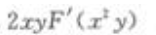
- B:
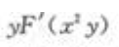
- C:
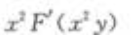
- D:
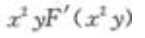
答 案:A
解 析:
主观题
1、设 存在二阶导数,求y'与y''.
存在二阶导数,求y'与y''.
答 案:解:
2、设事件A、B的概率分别为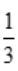 与
与 ,如果
,如果 ,求P(B
,求P(B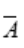 )的值;如果A与B互斥,求P(B
)的值;如果A与B互斥,求P(B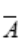 )的值;
)的值;
如果P(AB)=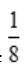 ,求P(B
,求P(B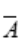 )的值.
)的值.
答 案:解:因P(A)=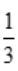 ,P(B)=
,P(B)= ,于是:(1)当
,于是:(1)当 时,P(B
时,P(B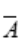 )=P(B-A)=P(B)-P(A)=
)=P(B-A)=P(B)-P(A)= .(2)当AB=
.(2)当AB=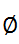 时,,从而B
时,,从而B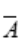 =B,P(B
=B,P(B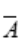 )=P(B)=
)=P(B)=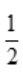 .
.
(3)当P(AB)= 时,则P(B
时,则P(B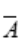 )=P(B)-P(AB)=
)=P(B)-P(AB)= .
.
填空题
1、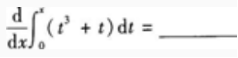 。
。
答 案:x3+x
2、 ()
()
答 案:0
解 析:令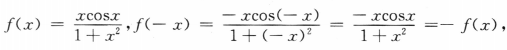 因此f(x)为奇函数,所以
因此f(x)为奇函数,所以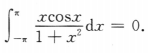
简答题
1、设函数y=y(x)是由方程cos(xy)=x+y所确定的隐函数,求函数曲线y=y(x)过点(0,1)的切线方程。
答 案:本题是一道典型的综合题,考查的知识点是隐函数的求导计算和切线方程的求法。 

解 析:
2、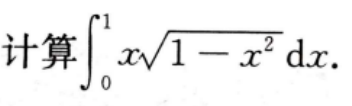
答 案: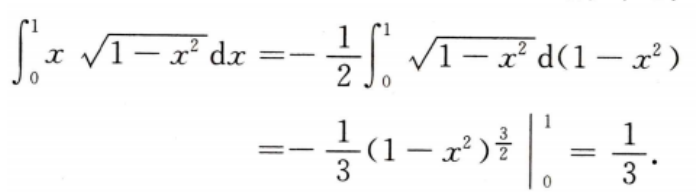
精彩评论