2025年成考专升本每日一练《高等数学一》3月18日专为备考2025年高等数学一考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、当x→0时,sinx·cosx与x比较是()。
- A:等价无穷小量
- B:同阶无穷小量但不是等价无穷小量
- C:高阶无穷小量
- D:低阶无穷小量
答 案:A
解 析: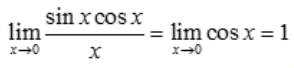 ,故sinx·cosx与x是等价无穷小量。
,故sinx·cosx与x是等价无穷小量。
2、设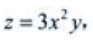 则
则 ()。
()。
- A:6dx+6dy
- B:3dx+6dy
- C:6dx+3dy
- D:3dx+3dy
答 案:C
解 析: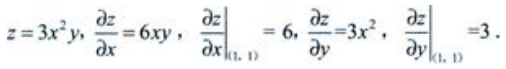
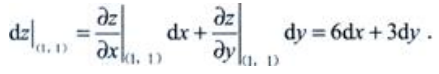
3、函数y=f(x)在点x0处可导的充分必要条件是()。
- A:它在该点处的左导数和右导数存在
- B:它在该点处连续
- C:它在该点处存在极限
- D:它在该点处可微
答 案:D
解 析:D项,对于一元函数来说,函数在某一点可导和在某一点可微等价.A项,函数在某一点的左导数和右导数存在且相等是函数在该点可导的充分必要条件.B项,可导一定连续,但连续不一定可导,例如函数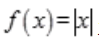 在x=0连续但不可导;C项,极限存在与函数存在不存在必然联系。
在x=0连续但不可导;C项,极限存在与函数存在不存在必然联系。
主观题
1、计算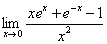
答 案: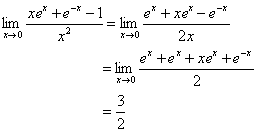
2、求
答 案:解: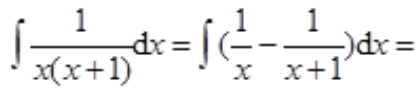
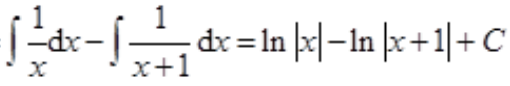
 。
。
3、设有一圆形薄片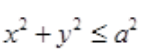 ,在其上一点M(x,y)的面密度与点M到点(0,0)的距离成正比,求分布在此薄片上的物质的质量。
,在其上一点M(x,y)的面密度与点M到点(0,0)的距离成正比,求分布在此薄片上的物质的质量。
答 案:解:设密度为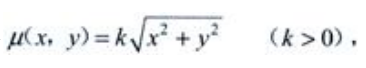 故质量
故质量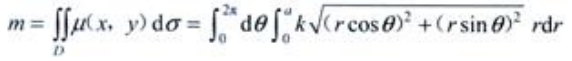

填空题
1、设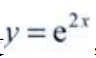 ,则
,则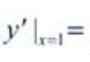 ()。
()。
答 案:2e2
解 析: ,则
,则
2、幂级数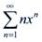 的收敛半径R=()。
的收敛半径R=()。
答 案:1
解 析:对于级数 ,
,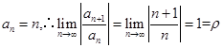 ,
,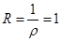 。
。
3、过点(0,1,1)且与直线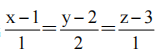 垂直的平面方程为()
垂直的平面方程为()
答 案:x+2y+z-3=0
解 析:由题意,平面法向量为n=(1,2,1),又过点(0,1,1),故方程为x+2(y-1)+(z-1)=0,即x+2y+z-3=0.
简答题
1、 (1)将f(x)展开为x的幂级数;
(1)将f(x)展开为x的幂级数;
(2)利用(1)的结果,求数项级数 的和。
的和。
答 案: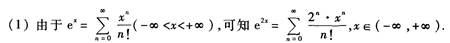 (2)在上述展开式中,令x=1,可得
(2)在上述展开式中,令x=1,可得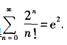
精彩评论