2025年成考专升本每日一练《高等数学二》3月11日专为备考2025年高等数学二考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、若，则。（）  

答 案：错

解 析：

单选题

1、设f(x)的一个原函数是arctanx，则f(x)的导函数是（）

• A：
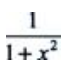
• B：
• C：
• D：

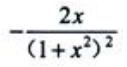
答 案：D

解 析：根据原函数的定义可知，则

2、当x→0时，x－sinx是x的（）.

• A：高阶无穷小
• B：等价无穷小
• C：同阶无穷小，但不是等价无穷小
• D：低阶无穷小

答 案：A

解 析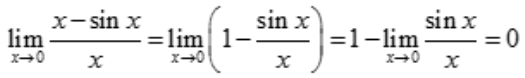：，所以当x→0时，x－sinx是x的高阶无穷小.

主观题

1、己知某篮球运动员每次投篮投中的概率是0.9，记X为他两次独立投篮投中的次数．（1）求X的概率分布；
（2）求X的数学期望EX．

答 案：解：（1）X可能的取值为0，1，2；因此X的概率分布为 （2）数学期望
EX＝0×0.1＋1×0.18＋2×0.81＝1.80

2、设曲线y＝cosx（0≤x≤π/2）与x轴、y轴所围成的图形面积被曲线y＝asinx，y＝bsinx（a＞b＞0）三等分，试确定a、b的值．

答 案：解：由y＝cosx，y＝asinx，得tanx＝1/a，故有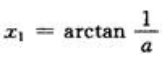；同理可求得.因为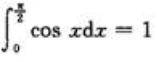，令这三部分的面积分别为D₁，D₂，D₃，有D₁＝D₂＝D₃＝1/3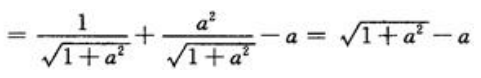．，故a＝4/3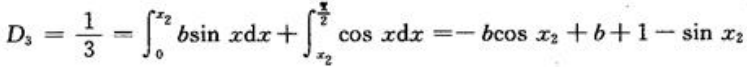．故b＝5/12．

填空题

1、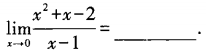  

答 案：2

解 析：

2、设函数，在x＝0处连续，则a＝（）．

答 案：2

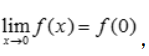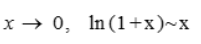
解 析：因为函数在x＝0处连续，故有由于所以a＝2．

简答题

1、求由曲线y=2-x²，y=2x-1及x≥0围成的平面图形的面积S以及此平面图形绕x轴旋转一周所得旋转体的体积V_x。  

答 案：本题考查的知识点有平面图形面积的计算及旋转体体积的计算。 本题的难点是根据所给的已知曲线画出封闭的平面图形，然后再求其面积S。求面积的关键是确定对x积分还是对y积分。确定平面图形的最简单方法是：题中给的曲线是三条，则该平面图形的边界也必须是三条，多一条或少一条都不是题中所要求的。确定对x积分还是对y积分的一般原则是：尽可能用一个定积分而不是几个定积分之和来表示。本题如改为对y积分，则有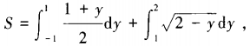

计算量显然比对x积分的计算量要大，所以选择积分变量的次序是能否快而准地求出积分的关键。
在求旋转体的体积时，一定要注意题目中的旋转轴是x轴还是y轴。
由于本题在x轴下面的图形绕x轴旋转成的体积与x轴上面的图形绕x轴旋转的旋转体的体积重合了，所以只要计算x轴上面的图形绕x轴旋转的旋转体体积即可。如果将旋转体的体积写成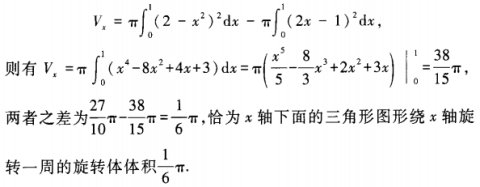

上面的这种错误是考生比较容易出现的，所以审题时一定要注意。
解由已知曲线画出平面图形为如图2-1-2所示的阴影区域。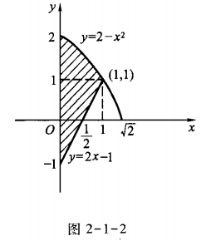

 

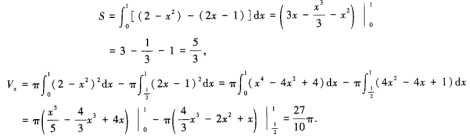
2、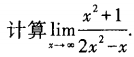  

答 案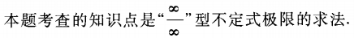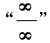： 型不定式极限的一般求法是提取分子与分母中的最高次因子，也可用洛必达法则求解。